Différences entre versions de « MOR - Modèle Océanique Régional »
| (5 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 20 : | Ligne 20 : | ||
=== Différences finies === | === Différences finies === | ||
| − | Les équations moyennées sur les couches sont résolues sur une grille tridimensionnelle où l'indice k croit avec l'axe des x, l'indice i | + | Les équations moyennées sur les couches sont résolues sur une grille tridimensionnelle où l'indice k croit avec l'axe des x, l'indice i décroit avec l'axe des y et l'indice j décroît avec l'axe des z. La résolution horizontale est constante, mais la résolution verticale est habituellement choisie afin de résoudre les gradients verticaux de densité et de courant. |
Les variables sont distribuées sur une grille Arakawa C montrée à la Figure 1 (Arakawa & Lamb, 1977<ref name='Arakawa_1977'>Arakawa, A., & Lamb, V. R. (1977). Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in computational physics, 17, 173-265.</ref>). L’unité fondamentale de calcul, la cellule, peut-être considérée comme un cube. Les courants sont calculés au centre des faces du cube et la salinité et la température sont définies au centre du cube. Les densités et les vitesses sont décalées dans l’espace afin que les gradients de densité soient centrés sur les vitesses. | Les variables sont distribuées sur une grille Arakawa C montrée à la Figure 1 (Arakawa & Lamb, 1977<ref name='Arakawa_1977'>Arakawa, A., & Lamb, V. R. (1977). Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in computational physics, 17, 173-265.</ref>). L’unité fondamentale de calcul, la cellule, peut-être considérée comme un cube. Les courants sont calculés au centre des faces du cube et la salinité et la température sont définies au centre du cube. Les densités et les vitesses sont décalées dans l’espace afin que les gradients de densité soient centrés sur les vitesses. | ||
[[Fichier:Arakawa-c.png|frame|right|800px|Figure 1: Grille Arakawa-c horizontale]] | [[Fichier:Arakawa-c.png|frame|right|800px|Figure 1: Grille Arakawa-c horizontale]] | ||
| Ligne 83 : | Ligne 83 : | ||
Pour lancer des simulations pluriannuelles, nous utilisons des script et gabarit pour ice_in et parrun. Ces scripts sont disponibles auprès de Simon Senneville. Ces fichiers sont habituellement dans un répertoire nommé ''Lance'' dans le répertoire ''RUN''. En exécutant la commande: | Pour lancer des simulations pluriannuelles, nous utilisons des script et gabarit pour ice_in et parrun. Ces scripts sont disponibles auprès de Simon Senneville. Ces fichiers sont habituellement dans un répertoire nommé ''Lance'' dans le répertoire ''RUN''. En exécutant la commande: | ||
qsub lance_job.pbs | qsub lance_job.pbs | ||
| − | Le script lancera gohsmodel_cice5. Gohsmodel_cice5 nécessite les | + | Le script lancera gohsmodel_cice5. Gohsmodel_cice5 nécessite les paramètres suivant: la date initiale, le nombre d'années voulues et si nous désirons démarrer la simulation à partir d'une simulation précédente. Par la suite, ce script modifiera, selon ses paramètres, les fichiers parrun.model et ice_in.model. Ces fichiers seront copiés dans ''RUN'' et la simulation sera lancée en arrière-plan à l'aide de gomodel. |
| − | À ce moment le fichier ''romstatus'' doit être présent et ne contenir que la valeur 0. Ce fichier ASCII indique si la dernière occurrence du modèle s'est terminée correctement (0) ou non (1). C'est nécessaire pour arrêter la boucle sur les années si le simulateur plante en cours de route. | + | À ce moment, le fichier ''romstatus'' doit être présent et ne contenir que la valeur 0. Ce fichier ASCII indique si la dernière occurrence du modèle s'est terminée correctement (0) ou non (1). C'est nécessaire pour arrêter la boucle sur les années si le simulateur plante en cours de route. |
===Créer un répertoire '''OUT''' dans votre environnement d'archivage=== | ===Créer un répertoire '''OUT''' dans votre environnement d'archivage=== | ||
| − | Ce répertoire contient les fichiers de sorties de la simulation. Il doit être situé sur un disque disposant de l’espace suffisant. | + | Ce répertoire contient les fichiers de sorties de la simulation. Il doit être situé sur un disque disposant de l’espace suffisant. À titre d'exemple, une solution horaire pour un an pour la baie d'Hudson (73x236x180) nécessite 400 Mb pour le fichier 2D et 4 Gb pour les fichiers 3D. |
==Traitement des fichiers de sortie de MOR sur Mingan== | ==Traitement des fichiers de sortie de MOR sur Mingan== | ||
| Ligne 94 : | Ligne 94 : | ||
===Fichier NetCDF=== | ===Fichier NetCDF=== | ||
| − | Les fichiers de sortie, comme la plupart des fichiers d'intrant, de MOR sont en format NetCDF. Par souci d'espace disque, ces fichiers ont été compressés sur un axe afin de ne conserver que les points mouillés. Le fichier NetCDF contient toutes les informations pour redistribuer ce vecteur sur la matrice 2D ou 3D du domaine. Avec la variable ''nwet(t,nwet_3D)'', où ''nwet_3D'' est le nombre d’éléments mouillés, qui contient les indices de la matrice initiale et data_nwet(tt,nj,ni,nk) qui contient les valeurs de la matrice, cette matrice peut être | + | Les fichiers de sortie, comme la plupart des fichiers d'intrant, de MOR sont en format NetCDF. Par souci d'espace disque, ces fichiers ont été compressés sur un axe afin de ne conserver que les points mouillés. Le fichier NetCDF contient toutes les informations pour redistribuer ce vecteur sur la matrice 2D ou 3D du domaine. Avec la variable ''nwet(t,nwet_3D)'', où ''nwet_3D'' est le nombre d’éléments mouillés, qui contient les indices de la matrice initiale et data_nwet(tt,nj,ni,nk) qui contient les valeurs de la matrice, cette matrice peut être reconstitué grâce à la boucle suivante: |
====Instructions pour décompresser le vecteur en matrice==== | ====Instructions pour décompresser le vecteur en matrice==== | ||
| Ligne 123 : | Ligne 123 : | ||
Des m-files ont été développés en Matlab pour lire et écrire dans ce format de fichier NetCDF. Voir Simon Senneville pour plus de détails. | Des m-files ont été développés en Matlab pour lire et écrire dans ce format de fichier NetCDF. Voir Simon Senneville pour plus de détails. | ||
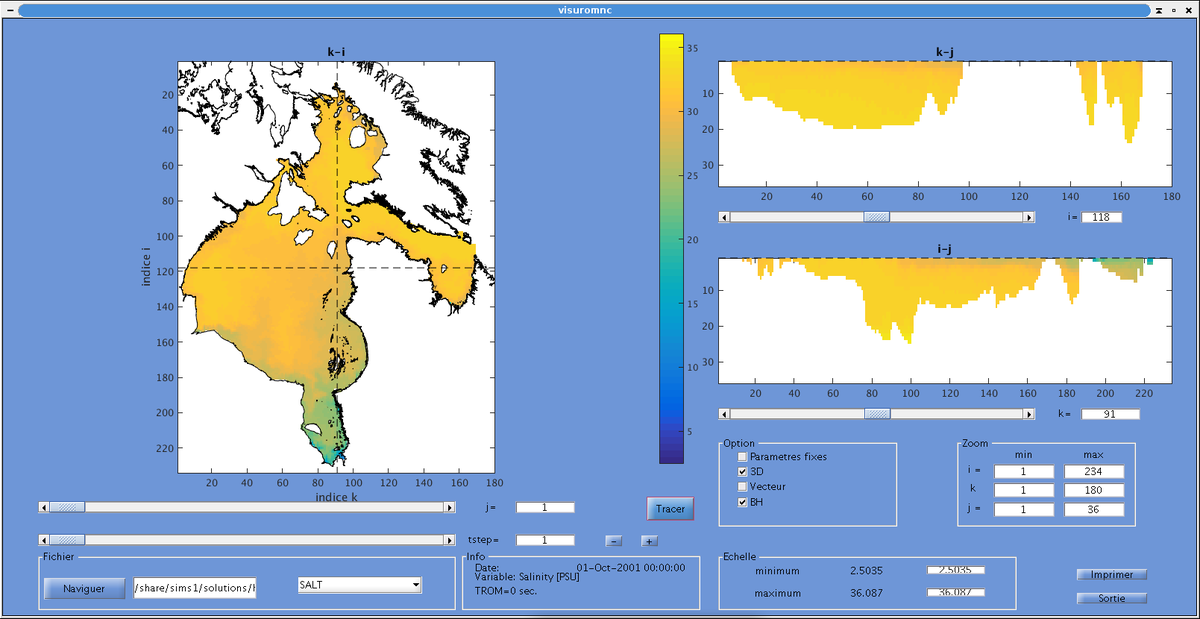
| − | [[Fichier:Visuromnc_exemple.png| | + | [[Fichier:Visuromnc_exemple.png|1200px|Exemple: Visuromnc pour le domaine de la baie d'Hudson]] |
Version actuelle datée du 28 juin 2017 à 10:53
Historique
Le modèle MOR utilise la base d’un modèle nommé GF8. Le modèle GF8 est la 8e version d'un modèle développé pour la région du détroit de Georgia, de Juan de Fuca et le Puget Sound près de Vancouver (Stronach et coll., 1993 [1]). Ce système est nommé Georgia-Fuca, d'où le nom du modèle. L’évolution du modèle MOR entraîne plusieurs différences par rapport à GF8, que ce soit au niveau du traitement du mélange, de la présence d’un modèle de glace couplé ou bien du transport des scalaires. Cependant, les équations de base ainsi que la technique de résolution restent quasiment les mêmes. Pour plus de détails sur la section suivante, veuillez consulter Stronach et coll. (1993)[1].
Description du modèle
Le modèle 3D glace de mer - océan calcule simultanément l'évolution spatiale et temporelle de l'énergie cinétique turbulente, des niveaux d'eau, des courants, des champs de température et de salinité des masses d'eau, de l'étendue et de l'épaisseur de la couverture de glace de mer. Le modèle océanique est à niveau-z entièrement pronostique, hydrostatique et basé sur les équations du mouvement en milieu peu profond modifiées de Backhaus (1983 [2]; 1985[3]) et Stronach et coll. (1993)[1]. Il utilise une solution semi-implicite pour l'élévation de surface, un schéma de transport corrigé pour les flux («flux-corrected», Zalezak, 1979 [4]) pour les grandeurs scalaires (température, salinité, énergie cinétique turbulente, variables biologiques), un mélange horizontal de faible valeur, et un modèle d'énergie turbulente d'ordre 2.5 (e.g. Burchard et Bolding, 2001 [5]; Smith et coll., 2006[6]) employant les fonctions de stabilité de Canuto et coll. (2001[7]). Le modèle d'énergie turbulente est complété par une équation diagnostique pour la balance d’échelle principale turbulente (utilisant le minimum entre la loi parabolique du mur et la longueur d'Ozmidov). Le modèle océanique est couplé à une couverture dynamique (Hunke et Dukowicz, 1997[8]) et thermodynamique (Semtner, 1976[9]) de glace de mer à deux couches, représentées par les distributions d'épaisseur d’après Thorndike et coll. (1975[10]) et une couche de neige. Les flux glace-océan, atmosphère-océan, et glace-atmosphère de la chaleur, du sel, et du momentum sont représentés par les formules aérodynamiques de Parkinson et Washington (1979[11]).
Implémentation du modèle numérique
Modèle de Hambourg
La technique utilisée pour solutionner les équations est celle de Backhaus (1985[3]), le modèle Hambourg. Les modes externes et internes sont traités de façon implicite et n'impose pas de restriction sur le pas de temps autre que la précision de la propagation de l'onde de marée. Voici quelques caractéristiques clés de ce modèle:
- La discrétisation dans le temps est partagée entre le mode implicite et explicite, habituellement moitié-moitié, ce qui en fait donc une méthode du second degré dans le temps. Augmenté ce facteur (donc plus implicite) permettrait de plus long pas de temps, mais au prix d'un amortissement de l’amplitude des ondes de courte période.
- La solution implicite des ondes gravitationnelles de surface est résolue par la technique SOR (Successive Over-Relaxation) appliquée à l’équation de continuité. Dans cette équation, la divergence du temps présent est combinée à la divergence du temps futur dans une proportion déterminée par le ratio de la contribution explicite et implicite discutée précédemment, pour déterminer la variation du niveau d’eau sur un pas de temps. La divergence du pas de temps futur est basée sur le niveau d’eau future, ce qui en fait une méthode implicite. L’équation de continuité est ultimement résolue comme une équation elliptique pour le champ de niveau d’eau du pas de temps futur.
- L'épaisseur des couches, bien que constante sur l'horizontale, peut varier sur la verticale.
Différences finies
Les équations moyennées sur les couches sont résolues sur une grille tridimensionnelle où l'indice k croit avec l'axe des x, l'indice i décroit avec l'axe des y et l'indice j décroît avec l'axe des z. La résolution horizontale est constante, mais la résolution verticale est habituellement choisie afin de résoudre les gradients verticaux de densité et de courant. Les variables sont distribuées sur une grille Arakawa C montrée à la Figure 1 (Arakawa & Lamb, 1977[12]). L’unité fondamentale de calcul, la cellule, peut-être considérée comme un cube. Les courants sont calculés au centre des faces du cube et la salinité et la température sont définies au centre du cube. Les densités et les vitesses sont décalées dans l’espace afin que les gradients de densité soient centrés sur les vitesses.
La forme du bassin est contrainte à avoir un nombre entier de cellules. La condition de transport nul à travers les parois du bassin est facilement respectée en imposant les vitesses sur la face de ces cellules formant la paroi à zéro. Le trait de côte détermine donc si la cellule sera dite mouillée, contenant de l’eau, ou bien sèche. Par la suite, c’est la profondeur en ce point mouillé qui détermine de nombre de cellules nécessaires. Nous ajoutons des cellules jusqu’à ce que la colonne d’eau soit égale à la profondeur. La cellule de surface et celle du fond sont d’épaisseur variable. Nous en discuterons plus en détail dans la section de construction d’une grille.
Méthode de solution
La solution d’un système complet d’équation de différence finie comporte 5 étapes.
1.L’équation de conservation est résolue afin de trouver le champ de vitesse verticale.
2.Le champ de densité est résolu en utilisant les vitesses verticales et horizontales au temps (0).
3.Les termes explicites des équations du mouvement sont évalués et ajoutés à une valeur intermédiaire des champs de vitesse u et v.
4.L’intégral vertical de l’équation de conservation est transformé en équation elliptique et résolue en utilisant SOR.
5.Les champs de niveau d’eau et de courant sont mis à jour à l’aide de la partie implicite des équations appropriées.
Comment utiliser MOR sur Mingan
Voici les quelques étapes nécessaires pour lancer une simulation de MOR sur Mingan. Dans un premier temps, il faut générer la structure des répertoires pour le code, l'exécutable et les solutions. Cette structure est donnée à titre d'exemple. Elle peut changer selon les besoins de chaque utilisateur.
Créer un répertoire SRC dans votre environnement de travail
Ce répertoire contient le code pour créer l'exécutable. Ce code est actuellement archivé sur un dépôt SVN. Ce code est disponible auprès de Simon Senneville. Vous modifierez très certainement ce code, il vous est suggéré d'utiliser GIT ou SVN pour gérer les différentes versions de votre code. Il est important de garder en tête qu'une fois votre développement terminé, il serait intéressant que les modifications puissent être traçables afin d'être récupérées et conservées pour les versions subséquentes du simulateur.
Générer l'exécutable
Le code source inclut un script qui génère une Makefile selon les options choisies du répertoire de configuration configure. Ce script se nomme make.comp. Il est appelé avec deux paramètres: le premier en fonction du serveur où il est utilisé et le second, en fonction du domaine voulu. Les configurations disponibles se retrouvent dans le répertoire configure. Pour ajouter de nouvelle configuration, elles doivent être ajoutées dans ce répertoire. Par exemple:
make.comp Cluster STLAW5KM
produira le fichier Makefile afin générer le simulateur du golfe du Saint-Laurent à 5km de résolution pour Mingan. Ensuite, il suffit de taper la commande make pour générer l'exécutable selon les instructions du Makefile.
Créer un répertoire RUN dans votre environnement de travail
Ce répertoire doit contenir l'exécutable et les fichiers nécessaires au lancement de MOR. L'exécutable est le résultat de la compilation de votre code. Si le fichier parrun est présent, cet exécutable pourrait être lancé directement, mais certaines variables d’environnement doivent préalablement être définies. De plus, certains scripts ont été développés pour traiter des aspects: interactif vs arrière-plan et l'utilisation des différents nœuds de la grappe. Habituellement, les modifications du code et la compilation se font sur le nœud de login de Mingan login-0-4. Cependant, AUCUN simulateur NE DOIT être lancé sur ce nœud. Le fichier parrun est essentiel au lancement du modèle. Ce fichier contient les paramètres essentiels du modèle ainsi que les informations sur les sorties voulues de la simulation, voici un exemple de fichier parrun. Si le modèle de glace CICE5 est utilisé, vous devez également avoir le fichier ice_in et deux répertoires vides soit restart et history.
Lancer la simulation sur un(des) nœud(s) interactif(s)
Sur la grappe de calcul Mingan, afin d'obtenir un nœud interactif vous devez utiliser
qsub -I suivie de -l nodes=X:ppn=Y
pour déterminer le nombre de nœuds et de processeurs voulu. Dans le cas suivant, votre demande pour 10 processeurs sur un nœud de calcul serait soumise. Par défaut, 10 Gig de mémoire sont alloués.
qsub -I -l nodes=1:ppn=10
Une fois sur votre nœud interactif, vous devez tout d’abord retourner dans votre répertoire RUN. Par défaut, vous serez dans votre home. Avant de lancer la simulation, des variables environnement doivent être définies, c'est fait à l'aide de module et de script. Vous devez donc charger les modules et script suivants:
module load dot
module load intel/compilateurs
module load netcdf/ifort
Maintenant vous pouvez lancer une simulation en mode interactif. Les sorties sur l'unité par défaut et les erreurs défileront à l'écran. Ce peut être utile pour le développent afin de suivre des traces dans le code. Cependant pour de longue simulations il est préférable de les lancer en arrière-plan. Une fois lancer en arrière-plan, ces sorties qui défilaient à l'écran seront enregistrées dans un fichier texte et votre simulation ne sera plus liée au terminal. Ne pas oublier de fermer votre session interactive une fois que vous en avez terminé en tapant exit dans le terminal.
Lancer la simulation sur un(des) nœud(s) en arrière-plan
De façon générale, voici les instructions pour soumettre une tâche sur Mingan. Notre fichier pbs devra contenir quelques instructions supplémentaires. Voici un exemple de lance_job.pbs. Pour lancer des simulations pluriannuelles, nous utilisons des script et gabarit pour ice_in et parrun. Ces scripts sont disponibles auprès de Simon Senneville. Ces fichiers sont habituellement dans un répertoire nommé Lance dans le répertoire RUN. En exécutant la commande:
qsub lance_job.pbs
Le script lancera gohsmodel_cice5. Gohsmodel_cice5 nécessite les paramètres suivant: la date initiale, le nombre d'années voulues et si nous désirons démarrer la simulation à partir d'une simulation précédente. Par la suite, ce script modifiera, selon ses paramètres, les fichiers parrun.model et ice_in.model. Ces fichiers seront copiés dans RUN et la simulation sera lancée en arrière-plan à l'aide de gomodel. À ce moment, le fichier romstatus doit être présent et ne contenir que la valeur 0. Ce fichier ASCII indique si la dernière occurrence du modèle s'est terminée correctement (0) ou non (1). C'est nécessaire pour arrêter la boucle sur les années si le simulateur plante en cours de route.
Créer un répertoire OUT dans votre environnement d'archivage
Ce répertoire contient les fichiers de sorties de la simulation. Il doit être situé sur un disque disposant de l’espace suffisant. À titre d'exemple, une solution horaire pour un an pour la baie d'Hudson (73x236x180) nécessite 400 Mb pour le fichier 2D et 4 Gb pour les fichiers 3D.
Traitement des fichiers de sortie de MOR sur Mingan
Fichier NetCDF
Les fichiers de sortie, comme la plupart des fichiers d'intrant, de MOR sont en format NetCDF. Par souci d'espace disque, ces fichiers ont été compressés sur un axe afin de ne conserver que les points mouillés. Le fichier NetCDF contient toutes les informations pour redistribuer ce vecteur sur la matrice 2D ou 3D du domaine. Avec la variable nwet(t,nwet_3D), où nwet_3D est le nombre d’éléments mouillés, qui contient les indices de la matrice initiale et data_nwet(tt,nj,ni,nk) qui contient les valeurs de la matrice, cette matrice peut être reconstitué grâce à la boucle suivante:
Instructions pour décompresser le vecteur en matrice
Pour chaque indice des pas de temps tstep Lire la variable nwet dimx=ny; % conversion de l'indice du fichier NetCDF à la matrice avec les indice du modèles dimy=nx; % conversion de l'indice du fichier NetCDF à la matrice avec les indice du modèles dimxy=nx*ny; Pour i = 1 : longeur(nwet) indice = double(floor(nwet(i))); indz = floor((indice-1) / dimxy); indice = floor(indice-indz*dimxy); indy = floor((indice-1) / dimx); indx = floor(indice-indy*dimx); indy = indy + 1 ; indz = indz + 1 ; data(tt,indz,indy,indx) = data_nwet(i); fin fin
Traitement à l'aide des librairies NetCDF
Voici un exemple de lecture de fichier NetCDF compressé en Fortran: lire_NetCDF
Traitement en Matlab
Des m-files ont été développés en Matlab pour lire et écrire dans ce format de fichier NetCDF. Voir Simon Senneville pour plus de détails.
- ↑ 1,0 1,1 et 1,2 Stronach, J. A., Backhaus, J. O., & Murty, T. S. (1993). An update on the numerical simulation of oceanographic processes in the waters between Vancouver Island and the mainland: the GF8 model. Oceanography and Marine Biology: An annual review, 31, 1-86.
- ↑ Backhaus, J. O. (1983). A semi-implicit scheme for the shallow water equations for application to shelf sea modelling. Continental Shelf Research, 2(4), 243-254.
- ↑ 3,0 et 3,1 Backhaus, J. O. (1985). A three-dimensional model for the simulation of shelf sea dynamics. Ocean Dynamics, 38(4), 165-187.
- ↑ Zalesak, S. T. (1979). Fully multidimensional flux-corrected transport algorithms for fluids. Journal of computational physics, 31(3), 335-362.
- ↑ Burchard, H., & Bolding, K. (2001). Comparative analysis of four second-moment turbulence closure models for the oceanic mixed layer. Journal of Physical Oceanography, 31(8), 1943-1968.
- ↑ Smith, G. C., Saucier, F. J., & Straub, D. (2006). Formation and circulation of the cold intermediate layer in the Gulf of Saint Lawrence. Journal of Geophysical Research: Oceans, 111(C6).
- ↑ Canuto, V. M., Howard, A., Cheng, Y., & Dubovikov, M. S. (2001). Ocean turbulence. Part I: One-point closure model—Momentum and heat vertical diffusivities. Journal of Physical Oceanography, 31(6), 1413-1426.
- ↑ Hunke, E. C., & Dukowicz, J. K. (1997). An elastic–viscous–plastic model for sea ice dynamics. Journal of Physical Oceanography, 27(9), 1849-1867.
- ↑ Semtner Jr, A. J. (1976). A model for the thermodynamic growth of sea ice in numerical investigations of climate. Journal of Physical Oceanography, 6(3), 379-389.
- ↑ Thorndike, A. S., Rothrock, D. A., Maykut, G. A., & Colony, R. (1975). The thickness distribution of sea ice. Journal of Geophysical Research, 80(33), 4501-4513.
- ↑ Parkinson, C. L., & Washington, W. M. (1979). A large‐scale numerical model of sea ice. Journal of Geophysical Research: Oceans, 84(C1), 311-337.
- ↑ Arakawa, A., & Lamb, V. R. (1977). Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in computational physics, 17, 173-265.