A Matlab package for georectifying oblique digital images (g rect)
Contents
- 1 Introduction
- 2 Condition of use and how to cite the g_rect package
- 3 How to get the package
- 4 Getting Started
- 5 g_calib
- 6 g_stablilize
- 7 References
- 8 Contributing authors
Introduction
This toolbox contains Matlab functions for georectifying highly oblique images. This is useful in oceanography for obtaining quantitative information on sea-surface patterns such as those induced by surface waves, internal waves, fronts, slicks, sea-ice, etc. Although this toobox was initially developed for the georectification of geophysical images it can be used just as well for rectifying laboratory images.
Condition of use and how to cite the g_rect package
The g_rect package is permanently stored and published as a compute capsule that follows best practices of reproducibility provided by the research collaboration platform Code Ocean. The g_rect compute capsule is published here: https://codeocean.com/capsule/6352444/tree
The only condition to use g_rect is that you agree to cite it in any publication, presentation or other work for which it was utilized.
The correct citation is:
Bourgault D, Pawlowicz R and Richards C (2020) g_rect : a MATLAB package for georectifying oblique images [Source Code]. https://doi.org/10.24433/CO.4037678.v1
How to get the package
There are 2 options to get the g_rect package.
- You can 'export' the code directly from the following address: https://codeocean.com/capsule/6352444/tree. The 'Export' option is found under the 'Capsule' menu on the top left of the main menu bar. This will download onto your computer a directory named like this: 4e339778-db0a-4cd1-a811-58f1b071bb12_v1. The code and the data are found within this directory and organized as described below.
- You can clone the code. In a terminal window, cd to the directory where you want your code to reside. Then type the following:
- > git clone https://git.codeocean.com/capsule-6352444.git
Once exported on cloned onto your computer, the g_rect package is organized as follow:
- code
- src (the source codes)
- g_rect (contains the main georectification functions)
- g_calib (contains camera calibration functions)
- g_stabilize (contains image stabilization functions)
- utilities
- m_map (Rick Pawlowicz's m_map package)
- uwit (functions that may be useful for image equalization)
- DNG2jpg (function to convert raw .DNG images to .jpg images)
- geotiffwrite_20121203 (function to write geotif images)
- Examples
- Example_1 (a field example with GCPs without any elevation)
- Example_2 (a field example with GCPs with elevations)
- Example_3 (a laboratory example)
- src (the source codes)
- environment (only contains a Dockerfile produced by Code Ocean. Not required for running g_rect.)
- metadata (only contains a file with metadata. Not required for running g_rect.)
The main georectification functions are found within the /src/g_rect/ directory.
The directories /src/g_calib/ and /src/g_stabilize/ are for more advanced processing if the camera needs to be calibrated or if a sequence of images need to be stabilized (i.e. remove small camera movements between successive images). More details on these below.
The directory /utilities/ contain other packages that are either required, such as the m_map package or are provided as utilities that may be useful for some more specific applications such as, for example, converting raw .DNG images into .jpg images (/src/utilities/DNG2jpg/).
Getting Started
The easiest way to get yourself familiar with g_rect is to go through and reproduce the examples provided and then adapt one of these examples to your particular situation.
The first thing to do is to set the entire /src/ directory and all of its subdirectories into your Matlab path (find the Set Path option in the Matlab menu). In principle, g_rect should run smoothly without the need of installing any other toolbox.
Example 1: Sea-ice in the St. Lawrence Estuary (Canada)
Go with Matlab into the directory /Examples/Example_1/. You will find there:
- the photo IMG_6614.JPG that shows a region of the St. Lawrence Estuary (Quebec) during winter.
- a file named g_rect_params.dat. This is the main input parameter file that is required by g_rect to perform the georectification. This is the file you will need to adapt for your particular application.
The parameter file provided with these examples are reasonably well documented. To get familiar with the package, please read the comments throughout this file which is explanatory. For this Example 1, the parameter file looks like this:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% The image found in this folder ('IMG_6614.JPG') was taken from the ski resort
% Massif de Charlevoix in Quebec (Canada). It shows sea-ice in the St. Lawrence
% Estuary. This image is not associated with any publication and is provided here
% only as an example for the use of the g_rect package.
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% INPUT/OUTPUT INFORMATION
% imgFname: This is the only image that will actually be treated
%
% firstImgFname: This is really just a comment not actually used by the algorithm
% that indicates the name of the first image of a sequence to which
% the georectification of image 'imgFname' could also be applied to.
%
% lastImgFname: Same as 'firstImgFname'but for the last sequential image.
%
% outputFname: This is the name of the output fil that will contain, among other
% variables, the matrices LON and LAT that will give the ground
% coordinate of every pixel of the image that are below the horizon.
%
imgFname = 'IMG_6614.JPG';
firstImgFname = 'IMG_6614.JPG';
lastImgFname = 'IMG_6614.JPG';
outputFname = 'IMG_6614_grect.mat';
%% FRAME OF REFERENCE
% The frame of reference could be either 'Geodetic' or 'Cartesian'.
% If 'Geodetic' is used, longitudes and latitudes are expected for positions.
% If 'Cartesian' is used, x-y positions are expected (in m)
%
frameRef = 'Geodetic';
%% CAMERA POSITION
% Set the longitude and latitude for ‘Geodetic’ frame of reference
% Set the x-y coordinate for ‘Cartesian’ frame of reference
%
LON0 = -70.6010167;
LAT0 = 47.2713000;
%% OFFSET
% Offset from center of the principal point (generally zero)
%
ic = 0;
jc = 0;
%% CAMERA PARAMETERS
% These are either the initial guesses for the uncertain parameters, i.e. those
% with an uncertainty > 0 (see next section) or the exact values for the parameters
% with an uncertainty set to 0 below.
%
% hfov: Field of view of the camera (degree)
% lambda: Dip angle (degree) below horizontal (e.g. straight down = 90, horizontal = 0)
% phi: Tilt angle (degree), generally close to 0.
% theta: View angle (degree) clockwise from North (e.g. straight East = 90)
% H: Camera altitude relative to the local water level (m)
%
hfov = 65;
lambda = 2;
phi = 0;
theta = 70;
H = 720;
%% UNCERTAINTIES
% Set here the uncertainties of the associated camera parameters.
% Set the uncertainty to 0 for fixed parameters.
%
dhfov = 20;
dlambda = 10;
dphi = 5;
dtheta = 20;
dH = 0;
%% POLYNOMIAL CORRECTION
% After the geometrical correction, a polynomial correction of degree 1 or 2
% could be applied. This could correct for some unknown distortions that cannot be
% corrected on geometrical grounds. Play carefully with this option as it is a purely
% mathematical fit which may lead to unphysical corrections or may hide other
% prior problems with the actual geometrical correction. Always first set this option
% to '0' in which case there will be no polynomial correction applied. In principle,
% the geometrical fit without this option should already be pretty good. You could then
% fine tune the image with this option. Be extra careful when using the second order
% polynomial fit, especially outside the region of the GCPs as the image could there
% be completely distorted.
%
polyOrder = 0;
%% PRECISION
% To save memory, calculations can be done in single precision.
% For higher precision set the variable 'precision' to 'double';
%
precision = 'double';
%% GROUND CONTROL POINTS (GCPs).
% The GCP data must come right after the 'gcpData = true' instruction
% Column 1: horizontal image index of GCPs
% Column 2: vertical image index of GCPs
% Column 3: longitude (Geodetic) or x-position (Cartesian) of GCPs
% Column 4: latitude (Geodetic) or y-position (Cartesian) of GCPs
% Column 5: elevation (in m) of GCPs (optional)
%
gcpData = true;
360 829 -70.561367 47.303783 0
54 719 -70.54500 47.335 0
99 661 -70.505 47.375 0
452 641 -70.435 47.389 0
429 633 -70.418 47.408 0
816 644 -70.393 47.368 0
This file contains all parameters required to perform a georectification. You can add spaces and comments as you wish within this file.
About Ground Control Points (GCPs)
In the parameter file, the GCPs must appear right after the variable gcpData = true in the format explained in the comment (i.e. 4 or 5 columns). These GCPs represent the positions (either in geodetic or cartesian coordinates) associated with some features seen in the image with known positions (a cape, a lighthouse, a wharf, a research boat, etc). These GCPs may have elevations as long as these elevations are below the horizon. Here, in this example, all GCPs are taken at the local water level. Example 2 below shows an example with GCPs with elevations.
About Camera Parameters
If you know perfectly some of the camera parameters (e.g. the field of view) you simply have to set the uncertainty of this parameter to zero (e.g. dfov = 0). The algorithm will use precisely this value. Otherwise, for other parameters with some uncertainties, the minimization algorithm will search within the given uncertainty range to find the parameter values that give a best fit between the image control points once georectified and the GCPs (see Bourgault, 2008, for details).
Running g_rect
To run the georectification, all you have to do in principle is to edit this parameter file for your particular application and to type g_rect at the Matlab command line. You will then be prompted to enter the name of the input parameter file (it does not have to be called g_rect_params.dat), like this:
Enter the name of the parameter file: g_rect_params.dat (or simply hit 'return' to use the default name)
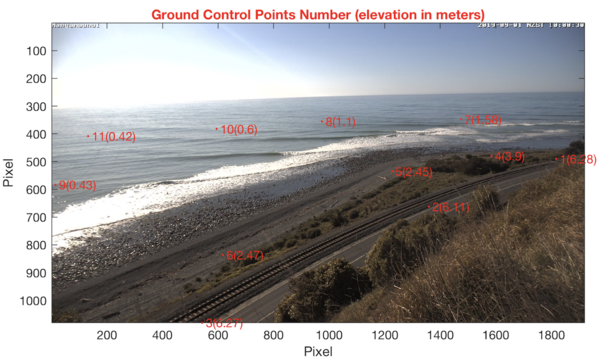
Your image will then appear with the GCPs. For this Example 1, this looks like this:
The red dots indicate the positions of the GCPs, sequentially numbered in the same order as they appear in the parameter file. The numbers in parentheses indicate the elevations (in m) of the GCPs. In this example, all GCPs are taken at water level so that all elevations are set to 0.
A table listing all of your parameters will also appear, like this:
INPUT PARAMETERS
Image filename: (imgFname):........... IMG_6614.JPG
First image: (firstImgFname):......... IMG_6614.JPG
Last image: (lastImgFname):........... IMG_6614.JPG
Output filename: (outputFname):....... IMG_6614_grect.mat
Image width (imgWidth):............... 1936
Image width (imgHeight):.............. 1288
Frame of reference:................... Geodetic
Camera longitude or x coord. (LON0):.. -70.601017
Camera latitude or y coord. (LAT0):... 47.271300
Principal point offset (ic):.......... 0.000000
Principal point offset (jc):.......... 0.000000
Field of view (hfov):................. 65.000000
Dip angle (lambda):................... 2.000000
Tilt angle (phi):..................... 0.000000
Camera altitude (H):.................. 720.000000
View angle from North (theta):........ 70.000000
Uncertainty in hfov (dhfov):.......... 20.000000
Uncertainty in dip angle (dlambda):... 10.000000
Uncertainty in tilt angle (dphi):..... 5.000000
Uncertainty in altitude (dH):......... 0.000000
Uncertainty in view angle (dtheta):... 20.000000
Polynomial order (polyOrder):......... 0
Number of GCPs (ngcp):................ 6
Precision (precision):................ double
You will then be asked if you are ok to proceed with the georectification, like this:
Is it ok to proceed with the rectification (y/n):
If so, type y and enter.
You will then see the algorithm searching the parameter space and to eventually return the results for the set of parameters found. The following information will appear on screen:
PARAMETERS AFTER GEOMETRICAL RECTIFICATION Field of view (hfov): 63.528162 Dip angle (lambda): 2.123610 Tilt angle (phi): 1.446089 Camera altitude (H): 720.000000 View angle from North (theta): 61.401050 The rms error after geometrical correction (m): 120.736597 Saving rectification file in: IMG_6614_grect.mat
A file will be created named according to the name provided by the variable outputFname. In this example, the file will be named IMG_6614_grect.mat. This is the main result file that contain the following variables:
Name Size Bytes Class Delta 1936x1288 19948544 double H 1x1 8 double LAT 1936x1288 19948544 double LAT0 1x1 8 double LON 1936x1288 19948544 double LON0 1x1 8 double errGeoFit 1x1 8 double errPolyFit 1x1 8 double firstImgFname 1x12 24 char frameRef 1x8 16 char h_gcp 1x6 48 double hfov 1x1 8 double i_gcp 1x6 48 double imgFname 1x12 24 char j_gcp 1x6 48 double lambda 1x1 8 double lastImgFname 1x12 24 char lat_gcp 1x6 48 double lat_gcp0 1x6 48 double lon_gcp 1x6 48 double lon_gcp0 1x6 48 double phi 1x1 8 double precision 1x6 12 char theta 1x1 8 double
Most of these variables have already been described in the parameter.dat file above and will not be repeated here.
The two most important matrices created are named LAT and LON. These two matrices have the same size as the original image and provide either the latitude-longitude pair of every pixel if you work with a Geodetic frame of reference, or the x-y pair (in m) if you work in a Cartesian frame of reference.
The output file also contains the horizontal positions and elevations of the GCPs used for the minimization algorithm stored in the variables lon_gcp, lat_gcp and h_gcp. A subtlety is that the output file also contains the variables lon_gcp0 and lat_gcp0. Here, in this Example 1 where there is no elevation associated with the GCPs, the variable lon_gcp0 is equal to lon_gcp and lat_gcp0 is equal to lat_gcp. It will become clearer in Example 2 below why these variable pairs may have different values when GCPs are provided with elevations.
The output file also contains the variable Delta which provides the effective resolution (in m) of the georectified image. Note that this resolution is highly spatially variable and irregular, with highest resolution in the foreground. For highly oblique images, the resolution deteriorates rapidly away from the camera. See Bourgault (2008, his equation 1) for details. This will become important in the next section.
Finally, g_rect produces the following figure that shows the resulting georectified image:
This image also shows the exact positions of the GCPs as blue circles while the red crosses show the position of the assoxiated pixel once georectified. A perfect fit would have the red crosses right on top of the blue circles. Here, in this example, we see some misfit that is quantified by the algorithm with
The rms error after geometrical correction (m): 120.736597
Effective resolution, re-interpolation, geotiff and worldfile
The function g_rect as ran above really produces the essential matrices LAT and LON. A figure is made at the end with the command pcolor implemented within the function g_viz_geodetic.m to show the resulting fit but that image is not necessarily what might be needed by most people, especially by those using Geographic Information Systems (GIS). What is often needed is a geotiff image or a jpeg image accompanied with a worldfile file (.jpw).
But to make a regular image, the resolution needs to be uniform whereas the effective resolution of the georectified image as produced by g_rect above is highly variable (see the variable Delta). Therefore, to produce a geotiff-type image, the data must be re-interpolated onto a regular grid. A choice (and a compromise) must then be made about the resolution. Re-interpolating the entire image at the highest resolution of the georectified data would likely produce an image that would be way too big in size. Generally, the image data are re-interpolated at an intermediate resolution, but the exact resolution is really a choice left to the user.
Two functions are provided with the g_rect package to produce either geotiff images or jpeg image plus a worldfile text file (.jpw). Note that these functions have only recently been developed and have not yet been fully tested and are not yet very general. You may need to play into the codes to make them work for your application. These are:
- g_geotiff.m
- g_jpg_jpw.m
For example, this figure shows the georectified data produced above by g_rect once re-interpolated on a regular 12 m x 12 m grid.
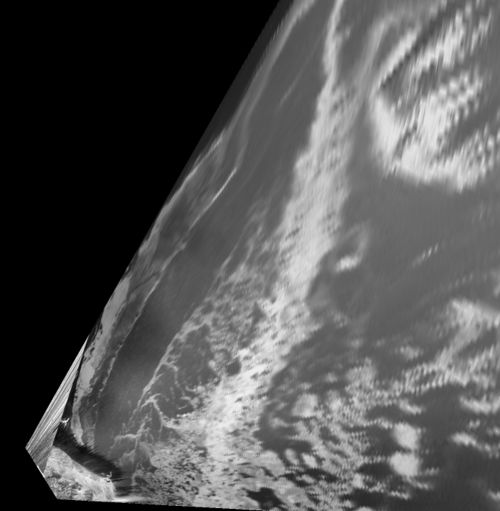
Example 2: Wave breaking on Mangamaunua Beach (New Zealand)
The second example provided can be found in the directory \Examples\Example_2\. The image and data for this second example were provided by Tom Shand from Tonkin + Taylor Ltd. The differences from the previous example are the following:
- the data are here given in Cartesian coordinates using the Universal Transverse Mercator system.
- GCPs have elevations. Indeed, some of the foreground GCPs were available at some height above the local sea level, some on the beach and some on the railway about 6 m above the sea level. Even the GCPs over water are elevated since they were obtained from hanging a sphere from a drone and were therefore not quite at height of the water level.
For this example, the parameter file is like this (note the different frame of reference used and the GCPs with elevations):
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% The image found in this folder ('Camera01.jpg') as well as the data found below in
% this parameter file were graciously provided by Tom Shand from Tonkin + Taylor Ltd.
% Auckland, New Zealand (www.tonkintaylor.co.nz).
%
% The reference for the image and the data is:
%
% Shand, T., Reinen-Hamill, R., Weppe, S. and A. Short (2019) Development of a
% framework for assessing effects of coastal engineering works on a surf break.
% Australasian Coasts and Ports Conference, September 2019, Hobart, Australia.
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% INPUT/OUTPUT INFORMATION
% imgFname: This is the only image that will actually be treated
%
% firstImgFname: This is really just a comment not actually used by the algorithm
% that indicates the name of the first image of a sequence to which
% the georectification of image 'imgFname' could also be applied to.
%
% lastImgFname: Same as 'firstImgFname'but for the last sequential image.
%
% outputFname: This is the name of the output fil that will contain, among other
% variables, the matrices LON and LAT that will give the ground
% coordinate of every pixel of the image that are below the horizon.
%
imgFname = 'Camera01.jpg';
firstImgFname = 'Camera01.jpg';
lastImgFname = 'Camera01.jpg';
outputFname = 'Camera01_grect.mat';
%% FRAME OF REFERENCE
% The frame of reference could be either 'Geodetic' or 'Cartesian'.
% If 'Geodetic' is used, longitudes and latitudes are expected for positions.
% If 'Cartesian' is used, x-y positions are expected (in m)
%
frameRef = 'Cartesian';
%% CAMERA POSITION
% Set the longitude and latitude for ‘Geodetic’ frame of reference
% Set the x-y coordinate for ‘Cartesian’ frame of reference.
%
LON0 = 1661768;
LAT0 = 5316087;
%% OFFSET
% Offset from center of the principal point (generally zero)
%
ic = 0;
jc = 0;
%% CAMERA PARAMETERS
% These are either the initial guesses for the uncertain parameters, i.e. those
% with an uncertainty > 0 (see next section) or the exact values for the parameters
% with an uncertainty set to 0 below.
%
% hfov: Field of view of the camera (degree)
% lambda: Dip angle (degree) below horizontal (e.g. straight down = 90, horizontal = 0)
% phi: Tilt angle (degree), generally close to 0.
% theta: View angle (degree) clockwise from North (e.g. straight East = 90)
% H: Camera altitude relative to the local water level (m)
%
hfov = 70;
lambda = 20;
phi = 0;
theta = 90;
H = 30;
%% UNCERTAINTIES
% Set here the uncertainties of the associated camera parameters.
% Set the uncertainty to 0 for fixed parameters.
%
dhfov = 10;
dlambda = 20;
dphi = 2;
dtheta = 10;
dH = 0;
%% POLYNOMIAL CORRECTION
% After the geometrical correction, a polynomial correction of degree 1 or 2
% could be applied. This could correct for some unknown distortions that cannot be
% corrected on geometrical grounds. Play carefully with this option as it is a purely
% mathematical fit which may lead to unphysical corrections or may hide other
% prior problems with the actual geometrical correction. Always first set this option
% to '0' in which case there will be no polynomial correction applied. In principle,
% the geometrical fit without this option should already be pretty good. You could then
% fine tune the image with this option. Be extra careful when using the second order
% polynomial fit, especially outside the region of the GCPs as the image could there
% be completely distorted.
%
polyOrder = 0;
%% PRECISION
% To save memory, calculations can be done in single precision.
% For higher precision set the variable 'precision' to 'double';
%
precision = 'double';
%% GROUND CONTROL POINTS (GCPs).
% The GCP data must come right after the 'gcpData = true' instruction
% Column 1: horizontal image index of GCPs
% Column 2: vertical image index of GCPs
% Column 3: longitude (Geodetic) or x-position (Cartesian) of GCPs
% Column 4: latitude (Geodetic) or y-position (Cartesian) of GCPs
% Column 5: elevation (in m) of GCPs (optional)
%
gcpData = true;
1818 490 1661903.38 5316012.52 6.28
1359 662 1661846.11 5316069.20 6.11
543 1080 1661802.48 5316102.36 6.27
1584 479 1661926.61 5316026.49 3.90
1226 535 1661902.92 5316070.64 2.45
617 836 1661828.83 5316109.15 2.47
1475 347 1662214.16 5315956.24 1.58
974 355 1662195.27 5316115.86 1.10
14 583 1661893.51 5316195.60 0.43
595 382 1662132.48 5316216.56 0.60
132 408 1662085.97 5316320.83 0.42
You can run g_rect with this parameter file. The image and the GCPs are like this:
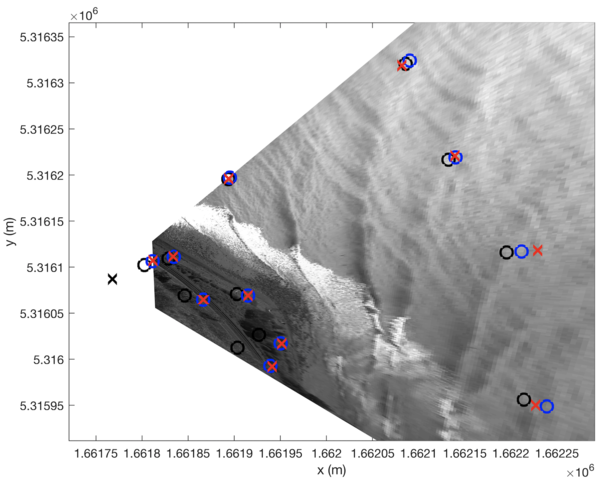
The georectified data are like this:
Note here the presence of the black circles that were absent in the previous example. These black circles are the position of the elevated GCPs, that is the position provided in the parameter file. These black circles correspond to the variables lon_gcp0 and lat_gcp0. However, since these GCPs have elevations, these positions are not exactly the one used by the minimization algorithm. Instead, the GCPs used are the projection of these GCPs onto the local water level along the line that joins the camera and the elevated GCP. These projected GCPs are the blue circles.
Once re-interpolated onto a regular grid using the function g_jpg_jpw.m, the image becomes:
The corresponding worldfile is like this:
1 0 0 -1 1661500 5316500
Example 3: A laboratory case
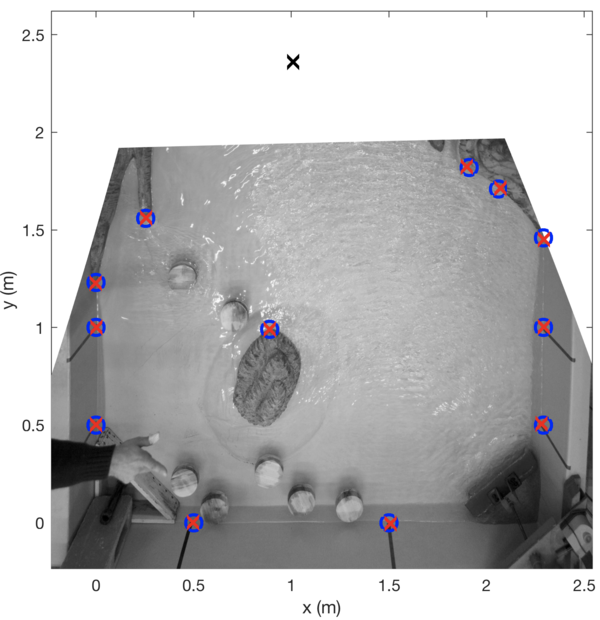
The third example provided, found in the directory \Examples\Example_3\, is a case that shows g_rect applied to the laboratory. There is nothing more special about this case that has not been seen in the the previous two examples. It's provided here so that it could be used as a starting point to someone who would like to apply the algorithm to the lab. Let's only note that the frame of reference used in the lab would normally be cartesian. The parameter file for this example is not relisted here but it is provided as in the other two previous examples.
Let's only show the image of the GCPs used for this case:
And the resulting rectification:
g_calib
Camera calibration could be done if required. All files needed are found in the g_calib folder. The package comes from this site that you should consult for information on how to perform a camera calibration: http://www.vision.caltech.edu/bouguetj/calib_doc/
Essentially, a camera calibration removes distortion associated with a lens. The images below shows the effect of such a camera calibration.
Note that this step is not always required for two main reasons. Firstly, it could be that the camera and lens you use has acceptable distortion. Secondly, the algorithm in g_rect provides a polynomial correction (of order 1 or 2) to the image if you have enough ground control points (it is the variable name polyOrder in the input parameter file). This is an indirect way of correcting for lens distortion that might be acceptable, especially if you have ground control points well spread within the image. However, the polynomial correction may be dangerous if your ground control points are clustered within a specific region of the image in which case unrealistic distortions may appear outside the region with ground control points.
g_stablilize
Generally, sequences of images are collected from a fixed tripod. For example, you may want to observe the movement of sea-ice over a semi-diurnal cycle at a sample rate of 1 image per minute (roughly 750 images). If the tripod does not move during the experiment then the georectification procedure described above with g_rect only needs to be applied to one image. The resulting coordinate matrices LAT and LON can then be applied to all images of the sequence.
In practice, the camera may move for many reasons. It may be because you needed to replace the batteries, because you touched the camera by mistake, because you needed to change a camera setting half-way through the experiment or, if you're outside, because wind gusts induced small but perceptible camera movements or if you use a drone. If you don't correct for these movements, the sequence will be jumpy if you make a movie with it. This may lead to inaccurate measurements if you need to compare two frames, say for calculating ice drift velocities (say using PIV) or internal wave phase speeds.
To fix this problem you could apply a new georectification to every images that has moved. This is however not practical if, for example, camera movements were randomly induced by wind gusts. In some windy situations, just about every image show small but perceptible camera movements. You wouldn't want to apply the georectification 100 or thousands of times.
This is when camera stabilization becomes very useful. The idea is to choose one reference image, generally the first image of the sequence, and to geometrically transform all other images, for translation, scale and rotation, to match as close as possible the reference image. This step is done on the normal photos, before doing the georectification.
For this to work properly we need to tell the algorithm which parts of the image are not supposed to have moved. The algorithm cannot tell by itself whether it is the camera that moved or the evolving feature we are documenting (moving ice, evolving fronts or internal wave propagation). These portions of the image that are not supposed to move (e.g. land, islands) are called region of interest (ROI). Details of the stabilizing procedure are described by Farid and Woodward (2007). The Matlab algorithm found in Farid and Woodward (2007) have been adapted here.
The folder g_stabilize contains a series of Matlab functions for performing the image stabilization. However, you need to be familiar with only the following two functions:
g_roi.m
This function is a utility that helps you determine region of interest. To use it you simply have to call the function with your reference image filename such as
g_roi('IMG_1.jpg')
and follow the instructions. Essentially, you will be asked to make polygons around regions of interests (roi). Those are regions in your image that are not supposed to show any movement. Make sure not to include any moving patterns on the water or the sky.
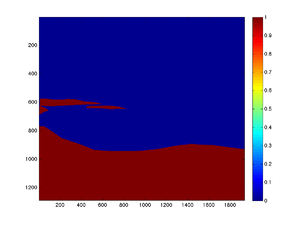
This function only puts 1s in ROIs and 0s everywhere else. Once you're done a file named roi.mat is created. The blue and red image below shows the ROI image corresponding to the image #1. This file is then needed by the next function that performs the actual stabilization.
g_stabilize.m
Once you have created the roi.mat file, copy this file in the folder that contains all images you wish to stabilize and then simply type, in principle, the following command:
g_stabilize(img_ref_fname)
where img_ref_fname is the name (with path and extension) of the reference image against which all images in the current directory will be stabilized against.
For example:
g_stabilize('IMG_2018.jpg')
if the images are in the current directory. Or perhaps
g_stabilize('experiment_1/data/IMG_2018.jpg')
if the images are located somewhere else.
The function will by default create a new directory called 'stable' (unless specified otherwise in the options) in which all images with the same name but with the suffix _stable (by default) will be created. The original images are conserved.
There is a number of options you may want to play with, such has the size of the L-level Gaussian pyramid (default is 4), or whether you want to equalize the image or whether you want to use the gradient of the image for stabilization. In general the stabilization algorithm works really well but it may require some trial and errors and some tweaking for any particular application. Type help g_stabilize to see the available options.
Remark
Because of rapidly changing light conditions outside, the stabilize algorithm may not always work as you would hope. This is because region of interests are often subject to moving cloud shadows that may fool the algorithm. In some cases it may be necessary to filter first you image and/or to apply equalizers in order to remove as much as possible such parasite motions. In general, the algorithm does quite a good job but may need some tweaking for some specific applications. You can appreciate the effect by downloading and comparing IMG_1.JPG with IMG_58.JPG and IMG_58_stable.JPG below.
References
Algorithm
- Bourgault (2008), Shore-based photogrammetry of river ice, Can. J. Civil Eng..
- Farid and Woodward (2007), Video stabilization and enhancement, Unpublished.
- Pawlowicz (2003), Quantitative visualization of geophysical flows using low-cost oblique digital time-lapse imaging, IEEE J. Ocean. Eng.
Application examples
- Bourgault, Galbraith and Chavanne (2016), Generation of internal solitary waves by frontally-forced intrusions in geophysical flows, Nat. Commun.
- Bourgault and Kelley (2003), Wave-induced boundary mixing in a partially-mixed estuary, J. Mar. Res..
- Bourgault et al (2011), Field observations of a large-amplitude internal wavetrain and its reflection off a steep slope, J. Phys. Oceanogr.
- Richards et al (2013), Measurements of shoaling internal waves and turbulence in an estuary, J. Geophys. Res.
- Wang and Pawlowicz (2011), Propagation speeds of strongly nonlinear near‐surface internal waves in the Strait of Georgia, J. Geophys. Res.
- Wang and Pawlowicz (2012), Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia, J. Geophys. Res.
Contributing authors
- Daniel Bourgault - Institut des sciences de la mer de Rimouski (email: daniel_bourgault@uqar.ca)
- Rich Pawlowicz - University of British Columbia (email: rich@eos.ubc.ca)
- Clark Richards - Bedford Institute of Oceanography (email: Clark.Richards@dfo-mpo.gc.ca)